栈和队列原理
栈和队列原理
Nuyoah栈和队列
定义:
- 栈和队列是两种常用的,重要的数据结构
- 栈和队列是限定插入和删除只能在表的“端点“进行的线性表
- 其中栈,规定再插入的时候只能插入在表尾,删除的时候也只能删除最后一个
- ”后进先出“ 是栈的结构特点
- 数值转换
- 表达式求值
- 括号匹配的检验
- 八皇后的问题
- 行编辑的程序
- 函数调用
- 迷宫求解
- 函数调用
- 迷宫求解
- 递归调用的实现
- 其中队列,规定插入的时候 只能在表尾插入,删除的时候只能在表头删除。
- ”先进先出“是队列的结构特点,使得队列可以解决类似排队问题的有用工具
- 脱机打印输出:按申请的先后顺序依次输出
- 多用户系统中,多个用户排成队,分时的循环使用CPU和主存
- 按用户优先级拍成多个队,每个优先级一个队列
- 实时控制系统中,信号按接受的先后顺序依次处理
- 网络电文传输,按照到达的时间先后顺序依次进行
- 其中栈,规定再插入的时候只能插入在表尾,删除的时候也只能删除最后一个
栈的结构和特点
栈是一个特殊的线性表,是限定仅在一段(通常是表尾)进行插入和删除操作的线性表
- 又称为后进先出(Last In First Out)的线性表,简称LIFO结构
栈的相关概念
-
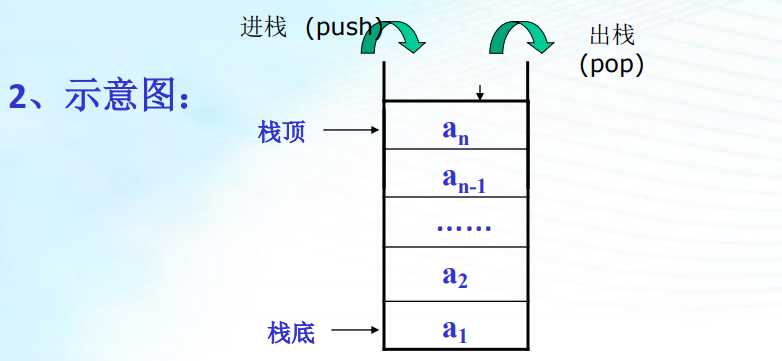
栈是仅在表尾进行插入,删除操作的线性表。表尾(即an端)称为栈顶Top;表头(即a1段)称为栈底Base(通常使用S来表示)
插入元素到栈顶(即表尾)的操作,称为入栈
从栈顶即(表尾)删除最后一个元素的操作,称为处栈
“入” = 压入 = PUSH “出” = 弹出 = POP
-
栈的定义和特点
- 假如有三个元素a,b,c,入栈顺序是a,b,c,则他们的出栈顺序有几种可能
- 先让abc依次进入,然后再依次出来结果 cba;
- a进出,a出来, b进入,b出来,c进入,c出来 结果 abc
- a进入, a出来, bc依次进入,bc依次出来, 结果 acb
- ab依次进入, ab依次出来,c进入,c出来 结果bac
- ab依次进入, b出来, c进入, ca依次出来, 结果 bca
-
栈的相关概念
- 定义:限定只能在表的一段进行插入和删除运算的线性表(只能在栈顶进行操作)
- 逻辑结构:与线性表相同,仍为一对一关系
- 存储结构:用顺序栈或链栈存储均可,但以顺序栈更常见
- 运算规则:只能在栈顶运算,且访问结点时按照后进先出(LIFO)
- 实现方式:关键是编写入栈和出栈函数,具体实现依顺序栈,或链栈的不同而不同z
队列定义和特点
队列是一种先进先出(First In First Out ---- FIFO)的线性表,在表的一端插入(表尾)在另一端(表头)删除
队列的定义和特点
- 定义:只能在表的一端进行插入运算,在表的另一端进行删除运算的线性表,(头删尾插)
- 逻辑结构:与同线性表相同,仍为一对一关系
- 存储结构:顺序队或链队,以循环顺序队更常见
- 运算规则:只能在队首和队尾运算,且访问结点时按照先进先出(FIFO)的原则
- 实现方式:关键是掌握入队和出队操作,具体实现依顺序队或链队的不同而不同
案例引入
-
进制转换(栈)
使用其后进先出的特性
例如这张图片 存入的时候时10111, 利用栈的特性, 输出11101, 正是我们想要的结果
-
括号匹配的检验(栈)
假设表达式中允许包含两种括号:圆括号和方括号
其嵌套顺序随意即
-
([] ()) 或 [([ ] [ ])] 为正确格式
-
[ ( ] ) 为错误格式
-
( [ ( ) ) 或 ( ( ) ] ) 为错误格式
例如检验 ( ( ) ] ) 是否匹配 :使用一个栈来解决这个问题
从左往右依次遍历, 如果是左括号 则放入第一个栈里,如果是右括号则和让栈中弹出一个元素和他比较,如果左右匹配,则让这两个都出栈, 在进行遍历,直到最后栈里没有元素的时候,或者遇到不匹配的时候退出
以下几种情况就可以得出括号不匹配
- 当遇到某一个右括号的时候栈已空,说明到目前为止,右括号多于左括号
- 从栈中弹出的左括号与当前检验的右括号不同说明出现括号交叉
- 算术表达式输入完毕,但栈中还没有匹配的左括号。说明左括号多余右括号
-
-
表达式求值(栈)
表达式求值是程序设计语言编译中一个最基本的问题,它的实现也需要用栈
这里使用算符优先算法
需要两个栈
一个是算符栈OPTR,用于寄存运算符。
另一个称为操作数栈OPND,用于寄存运算数和运算结果
求值的处理过程是自左至右扫描表达式的每一个字符
- 当扫描的是运算数,则将其压入栈OPND
- 当扫描到的是运算符时:
- 若这个比OPTR栈顶运算符优先级高,则入栈OPTR,继续向后处理
- 若这个运算符比OPTR栈顶运算符优先级低或同级则从OPTR中弹出栈顶运算符进行运算,并将其运算结果压入栈OPND
- 继续处理当前字符,直到遇到结束字符为止
-
舞伴问题(队)
两队,一队男,一堆女, 从开头依次配对, 两队人数可能不同,多的那一队,等待下一支舞曲,就能够优先配对
先进先出
栈的表示和操作的实现
栈的抽象数据类型的定义
ADT Stack
{
数据对象:
D = {ai | ai ∈ ElemSet, i = 1,2,.....n, n ≥ 0}
数据关系:
R1 = {<ai - 1 , ai > | ai-1, ai ∈ D, i = 2,.......,n, }
基本操作:
初始化,进栈, 出栈, 取栈顶元素等
}ADT Stack
InitStack(&S) 初始化操作
操作结果:构造一个空栈S
DestroyStack(&S) 销毁栈操作
初始条件:栈S已经存在。
操作结果:栈S被销毁。
StackEmpty(S) 判定S是否为空栈
初始条件:栈S已存在。
操作结果:若栈S为空栈,则返回True, 否则返回False
StackLength(S) 求栈的长度
初始条件:栈S已存在
操作结果:返回S的元素个数,即栈的长度
GetTop(S, &e) 获取栈顶元素
初始条件:栈S已存在且非空
操作结果:用e返回栈顶元素
ClearStack(&S) 清空栈
初始条件:栈S已经存在
操作结果:将S清为空栈
Push(&S, e) 入栈(压栈)操作
初始条件:栈S存在
操作结果:插入数据e为新的栈顶元素
Pop(&S, &e) 处栈操作
初始条件:栈S已存在且非空
操作结果:删除S栈顶元素an,且用e返回其值
由于栈本身就是线性表,于是栈也有顺序存储和链式存储两种实现方式
- 栈的顺序存储----顺序栈
- 栈的链式存储----链栈
顺序栈的表示和实现
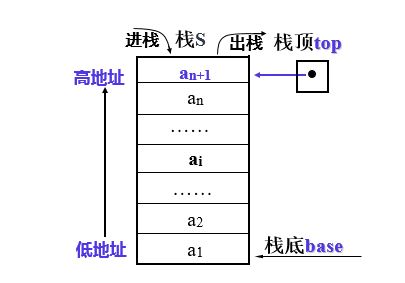
**存储方式**:同一般线性表的顺序存储结构完全相同,利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素,栈底一般在低地址端。
-
附设top指针,指示栈顶元素在顺序栈中的位置。
- 但是为了方便,通常top指示真正的栈顶元素之上的下标的地址
-
另设base指针,指示栈底元素在顺序栈中的位置
-
另外用stacksize表示栈可使用的最大容量
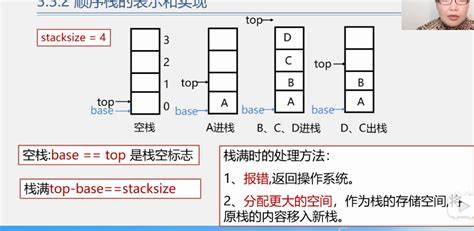
空栈: base == top 是栈空标志
栈满: top - base == stacksize
栈满的时候处理方法
-
报错, 返回操作系统
-
分配更大的空间,作为栈的存储空间,将原栈内容移入新栈
使用数组作为顺序栈的存储方式的特点
简单,方便,但易产生溢出(数组大小固定)
上溢:栈已满,又要压入元素
下溢:栈已空,还要弹出元素
注:上溢是一种错误,使问题的处理无法进行;而下溢是一种结束条件,即问题处理结束
顺序栈的表示
1 |
|
在栈中:
stacksize : 5;
top : 2;
base : 0;
栈中元素个数: = top - base = 2;
这里的相减是整数相减,但是我们上面设置的top和base是指针, 不过不影响,只要这两个指针类型相同,则它们相减,得出结果为这两指针之间的差;
顺序栈的初始化
1 | Status InitStack(SqStack *S) |
算法补充
-
判断顺序栈是否为空
1
2
3
4
5
6
7
8
9
10
11Status StackEmpty(SqStack S)
{
if(S.top == S.base)
{
return TRUE;
}
else
{
return FALSE;
}
} -
求顺序栈的长度
1
2
3
4int StackLength(SqStack S)
{
return S.top - S.base;`
} -
清空顺序栈
1
2
3
4
5
6
7
8Status ClearStack(SqStack S)
{
if(S.base)
{
S.top = S.base;
}
return OK;
} -
销毁顺序栈
1
2
3
4
5
6
7
8
9
10Status DestoryStack(SqStack *S)
{
if(S->base)
{
free(S->base);
S.stacksize = 0;
S.base = S.top = NULL;
}
return OK;
} -
顺序栈的入栈
判断是否栈满,若满则出错(上溢)
元素e压入栈顶
栈顶指针加1
1 | Status Push(SqStack *S, SElemType e) |
- 顺序栈的出栈
-
判断是否栈空,若空则错(下溢)
-
先将top指针向下移
-
取出栈顶的位置存在一个变量中方便返回
1 | Status Pop(SqStack S, SElemType e) |
栈的链式表示和实现
链栈是**运算受限**的单链表,只能在**链表头部**进行操作
1 | typedef struct StackNode |
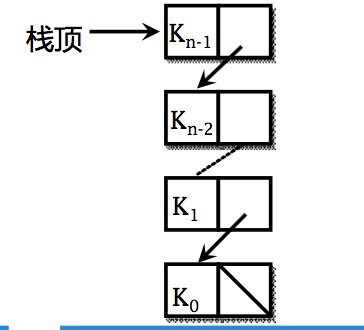
链栈中链表的指针方向都是从后指向前的 ,为了方便操作
- 链表的头指针就是栈顶
- 不需要头结点
- 基本不存在栈满的情况
- 空栈相当于头指针指向空
- 插入和删除仅在栈顶处执行
链栈的实现
- 链栈的初始化
1 | Status initStack(LinkStack *S) |
- 判断链栈是否为空
1 | Status StackEmpty(LinkStack S) |
- 链栈的入栈
1 | Status Push(LinkStack *S, SElemType e) |
- 链栈的出栈
1 | Status Pop(LinkStack *S, SElemType *e) |
- 取栈顶元素
1 | SElemType GetTop(LinkStack S) |
递归
递归问题----用分治法求解
分治法:对于一个较为复杂的问题,能够分解成几个相对简单的且解法相同或类似的子问题来求解
必备的三个条件
- 能将一个问题转换成一个新问题,而新问题与原问题的解法相同或类同,不同的仅是处理的对象,且这些处理对象是变化有规律的
- 可以通过上述转化而使问题简化
- 必须有一个明确的递归出口,或称递归边界
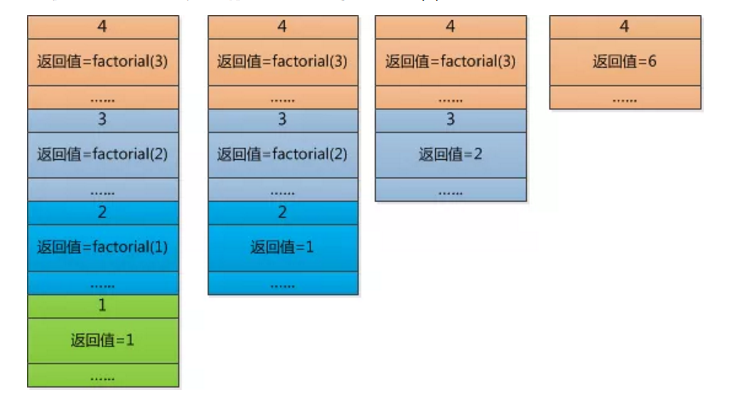
函数调用过程
- 调用前,系统完成:
- 将实参,返回地址等传递给被调用的函数
- 为被调用函数的局部变量分配存储区
- 将控制转移到被调用函数的入口
- 调用后,系统完成
- 保存别调用函数的计算结果
- 释放被调用函数的数据区
- 依照被调用函数保存的返回地址将控制转移到调用函数中
递归的优缺点
- 优点:结构清晰,程序易读
- 缺点:每次调用要生成工作记录,保存状态信息,入栈;返回时要出栈,恢复状态信息。时间开销大
递归->非递归
-
尾递归,单向递归 ->循环结构
- 尾递归->循环结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16long Fact(long n)
{
if(n == 0)
return 1;
else
return n * Fact(n-1);
}
long Fact(long n)
{
long t = 1;
for( i = 1; i <= n; i++)
{
t = t*i;
}
return t;
}- 单项递归->循环结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31long Fib(long n)
{
if( n == 1 || n == 2)
{
return 1;
}
else
{
return Fib(n-1) + Fib(n-2);
}
}
long Fib(long n)
{
if(n == 1 || n == 2 )
{
return 1;
}
else
{
t1 = 1;
t2 = 2;
for(i = 3; i <= n;i++)
{
t3 = t1 + t2;
t1 = t2;
t2 = t3;
}
return t3;
}
} -
自用栈模拟系统的运行时栈
借助栈改写递归
- 递归程序在执行的时候需要系统提供栈来实现
- 仿照递归算法执行过程中递归工作栈的状态变化可以写出相应的非递归程序
- 改写后的非递归算法与原来的递归算法相比,结构不够清晰,可取性较差,有的含需要经过一系列的优化
队列的表示和操作的实现
相关术语:
-
队列是尽在表尾进行插入操作,在表头进行删除操作的线性表
-
表尾即an端,称为队尾;表头即a1端,称为队头
-
它是一种先进先出(FIFO)的线性表
-
插入元素称为入队, 删除元素称为出队
-
队列的存储结构为链队或者顺序对(常用循环顺序队)
栈的物理存储可以用顺序存储结构,也可以是链式存储结构,相应的队列的存储方式也分为两种,即顺序队列和链式队列
队列的顺序表示—用一维数组base[MAXQSUZE]
1 |
|
队列的空满表示
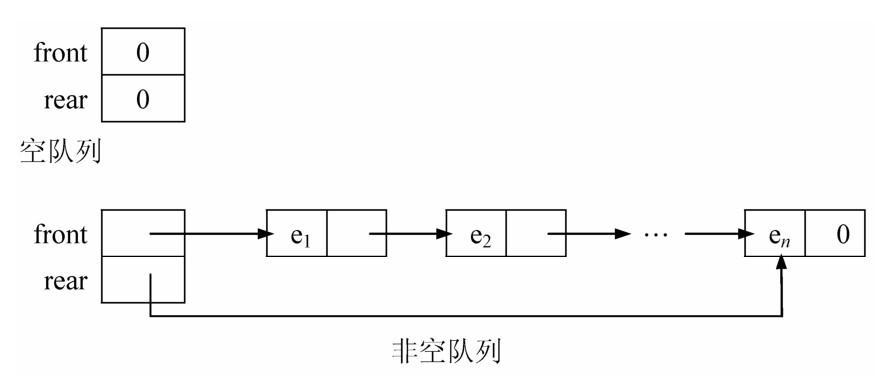
初始条件:front = rear = 0;表示队空
a :表示空队列
b:表示J1, J2, J3相继入队列; Q.rear分别++;
c:J1, J2相减被删除(这里图有错误Q.front 应指向J3) Q.front++;
d:这里表示J4,J5,J6插入队列之后,J3,J4被删除;
在进行到d的时候能否再进行插入???????
当Q.rear == MAXQSIZE时,发生溢出
- 若front = 0, rear = MAXQSIZE时 再入队— 真溢出
- 当rear = MAXQSIZE时 front != 0,时队列中还有空位,这是假溢出;
解决假上溢的方法
-
将队中元素依次向对头方向移动
缺点:浪费时间。每移动一次, 队中元素都要移动。
-
将队空间设想成一个循环的表,即分配给队列中m个存储单元可以循环使用,当rear为maxqsize时,若向量的开端空着,又可以从头使用空着的空间,当front为maxqsize时也是一样
-
引入循环队列
-
当rear == maxqsize的时候,就让他返回
-
实现方法:利用模(mod, %)运算。
-
插入元素Q.base[Q.rear] = x;
Q.rear = (Q.rear + 1)% MAXQSIZE;
-
插入元素:x = Q.base[Q.front]
Q,front = (Q.front + 1) % MAXQSIZE
-
-
这时候队满和队空都是一样的条件 front = rear
解决方法
- 另设置一个表示,以区分队空,队满
- 另设一个变量,记录元素的个数
- 少用一个空间(有n个空间 使用n-1个)
- 这时候队空时front = rear
- 队满时 (rear+1)%MAXQSIZE == front
循环队列类型定义
1 |
|
- 循环队列的操作----队列的初始化
1 | Status InitQueue(SqQueue *Q) |
- 循环队列的操作-------求队列的长度
1 | int QueueLength(SqQueue Q) |
- 循环队列------入队
1 | Status EnQueue(SqQueue *Q, QElemType e) |
- 循环队列-----循环队列出队
1 | Status DeQueue(SqQueue *Q, QElemType *e) |
- 取队头元素
1 | SElemType GetHead(SqQueue *Q) |
- 链队列的操作 ----- 链队列的初始化
1 | Status InitQueue(LinkQueue *Q) |
-
链队列的操作----销毁链队列
- 算法思想,从队头结点开始,依次释放所有节点
1
2
3
4
5
6
7
8
9
10Status DestroyQueue(LinkQueue *Q)
{
while(Q.front)
{
p = Q.front->next;
free(Q.front);
Q.front = p;
}
return OK;
} -
链队的操作----将元素e入队
1 | Status EnQueue(LinkQueue *Q, QElemType e) |
- 链队的操作—出队
1 | Status DeQueue(LinkQueue *Q, QElemType *e) |
- 链队列的队头元素
1 | Status GetHead(LinkQueue Q, QElemType *e) |