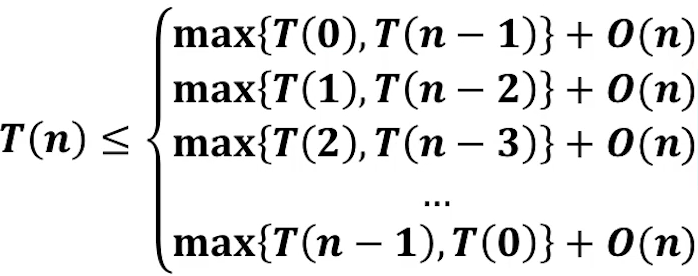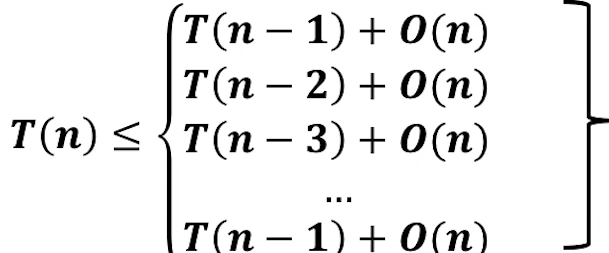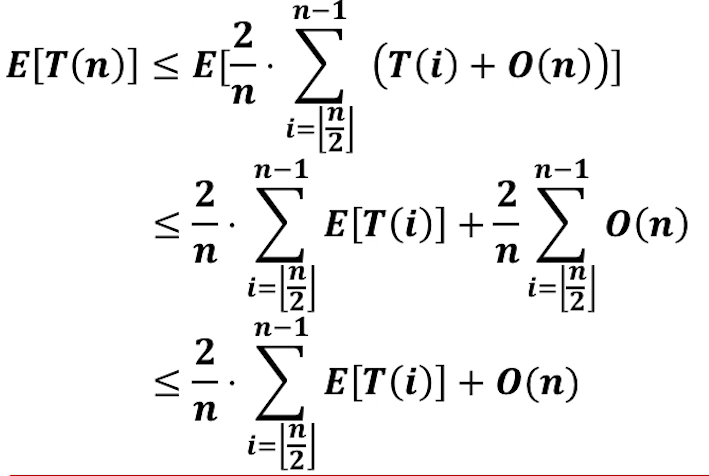次序选择问题

次序选择问题
Nuyoah次序选择问题
分析
问题输入:
-
包含n个不同元素的数组A[1…n]
-
整数k(1<k <n)
问题输出:
- 返回整数k的下标
问题求解:
- 蛮力法:
我们先把数据进行排序,然后我们想要第几个元素我们就选取第几个元素, 这样的时间复杂度为n * log(n) ,但是这样我们不仅得到了第i小的元素,而且我们还得到了第i+1 … 等一系列数据。这样就白白浪费了很多的时间。
- 改进快速排序法:
利用快速排序的思想,有以下几种情况:
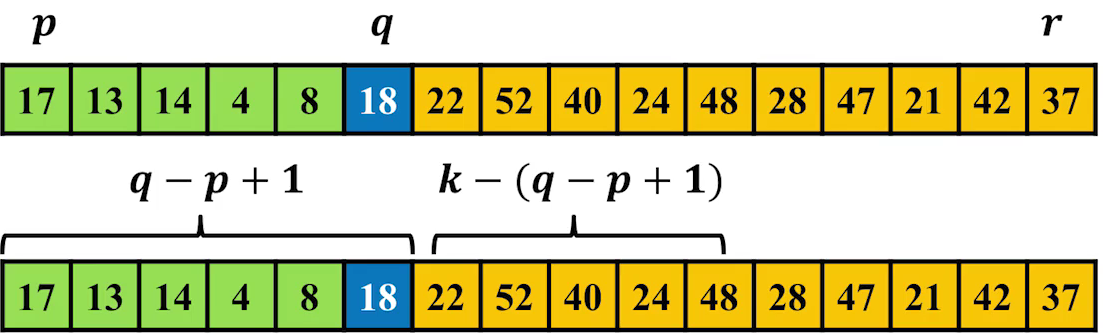
选取固定位置主元,小于主元的元素个数q-p。
- 情况1 : k =q- p + 1,A[q]为数组第k小元素
- 情况2 : k<q-p+ 1,在A[p…q -1]中寻找第k小元素
- 情况3 : k > q-p+1,在A[q+ 1…r]中寻找第k -(q -p+1)小元素
如果是情况一的话直接返回就行
如果是情况二的话我们就需要在 A[p…q -1]中寻找第k小元素
如果是情况三的话我们就需要在A[q+ 1…r]中寻找第k 小元素
解决问题的步骤为:
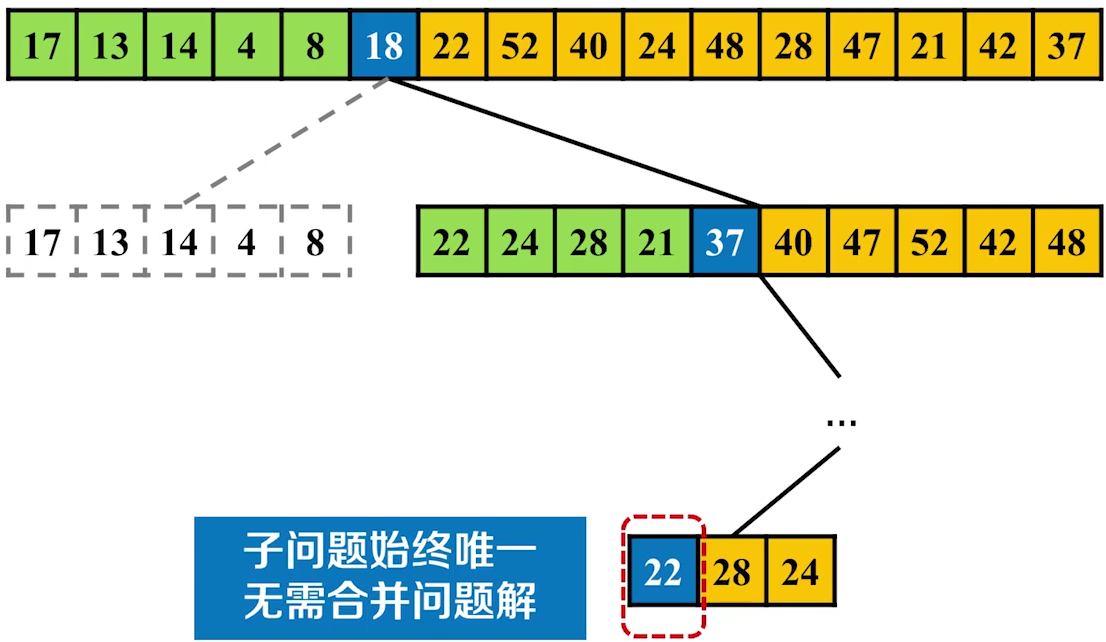
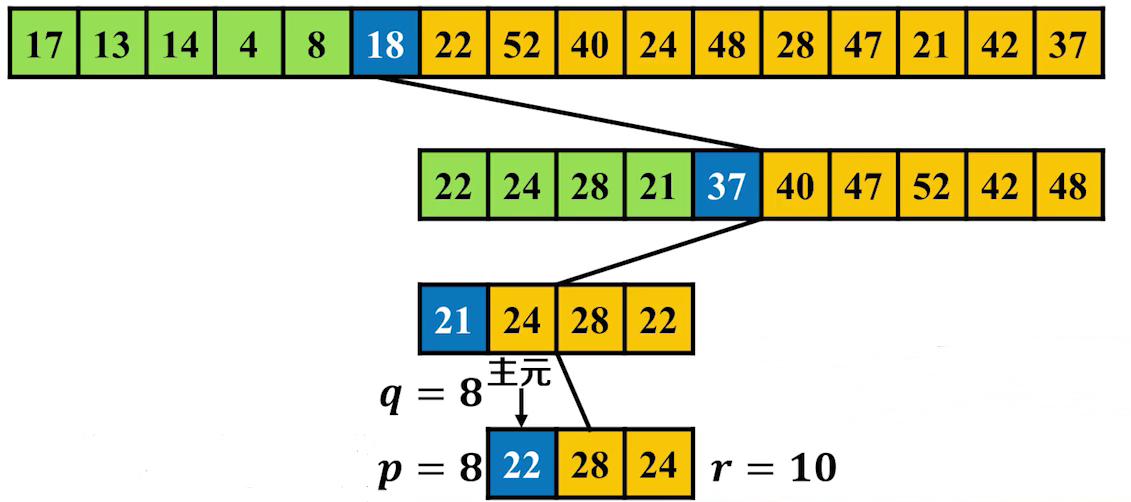
例题
如果我们需要查找第八小的元素
- 情况1 : k =q- p + 1,A[q]为数组第k小元素
- 情况2 : k<q-p+ 1,在A[p…q -1]中寻找第k小元素
- 情况3 : k > q-p+1,在A[q+ 1…r]中寻找第k -(q -p+1)小元素
时间复杂度
- 最好情况 :我们第一次就找到了第k小元素,
- 时间复杂度为:寻找出第k小的元素的时间复杂度:O(n)
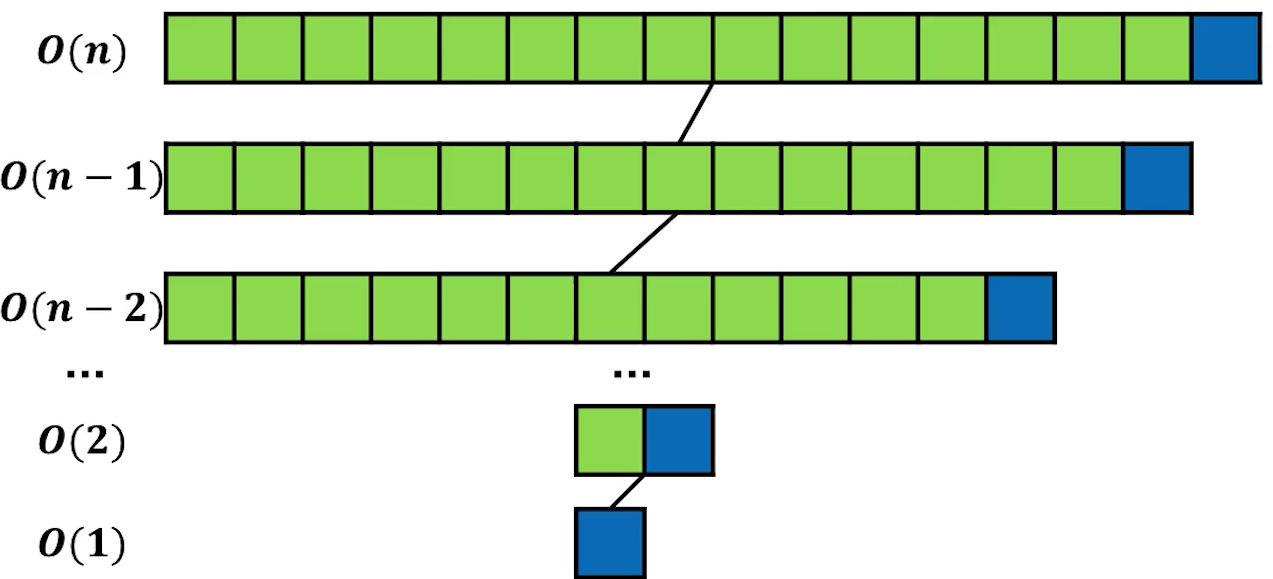
- 最坏情况orange :我们的所拥有的数组元素是一个已经排好序的
- 时间复杂度为:T(n) = O()
| 算法名称 | 最好时间复杂度 | 最坏时间复杂度 |
|---|---|---|
| 固定位置快速选择排序 | O() | O() |
| 固定位置次序选择问题 | O(n) | O() |
- 如何拜托最坏情况的困境? 使用随机位置划分
- 由于使用随机位置选择,我们无法直接求出这种方法的时间复杂度为多少,但是我们可以求出这个方法的期望时间复杂度
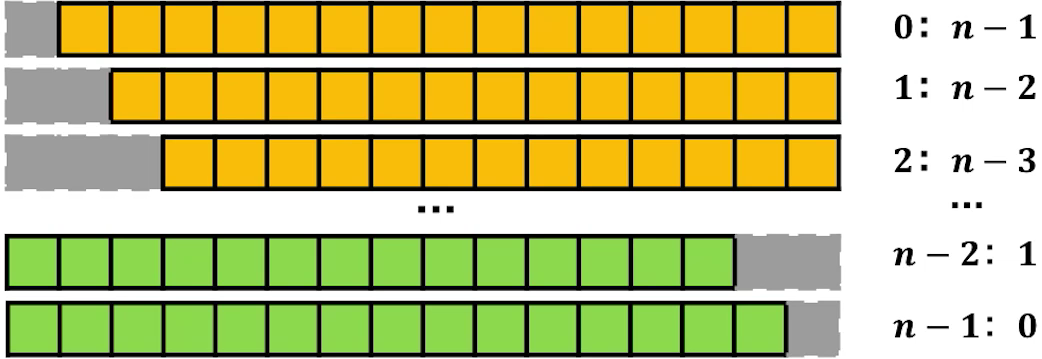
这里的时间复杂度我们可以选择较长的部分进行数组划分
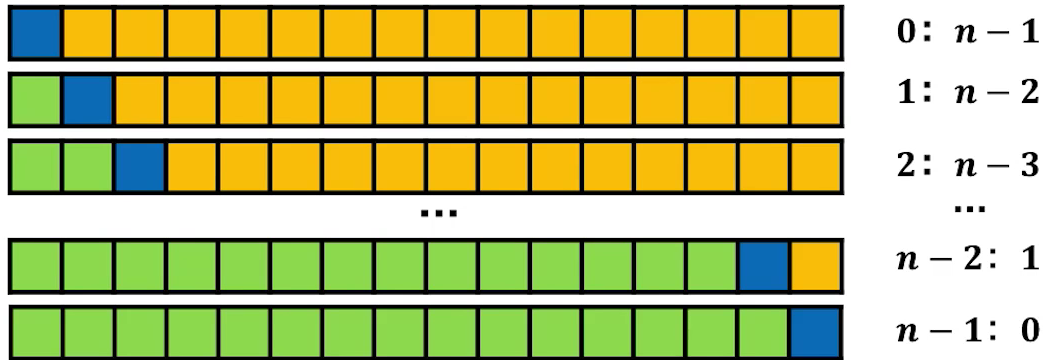
当我们选择较长的部分进行数组划分的时候会出现以下这种情况:
时间复杂度为:
我们观察这时间复杂度的式子可以发现这个时间复杂度的关系式是对称的 。一共有n种情况,每种情况出现的概率为1/n,出现次数为2次orange
期望时间复杂度为:
时间复杂度推理
我们由快速选择排序的 期望时间复杂度 = 最好时间复杂度,这个事实来猜测次序选择的既往时间复杂度也等于 最好时间复杂度
然后通过带入法来求证:
- 我们先猜想它的渐进紧确界,为O(n),然后来证明这个是它的渐进紧确界
- 证明 :存在c1, c2, n0 > 0,使得 任意n > n0, c1 * nlogn ≤ T(n) ≤ c2, * nlogn
代码
1 | import random |
评论
匿名评论隐私政策
✅ 你无需删除空行,直接评论以获取最佳展示效果