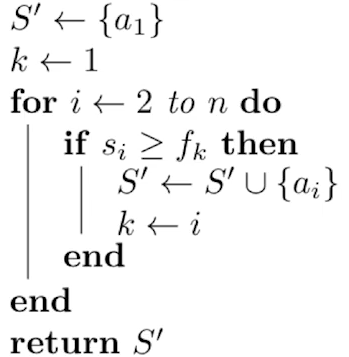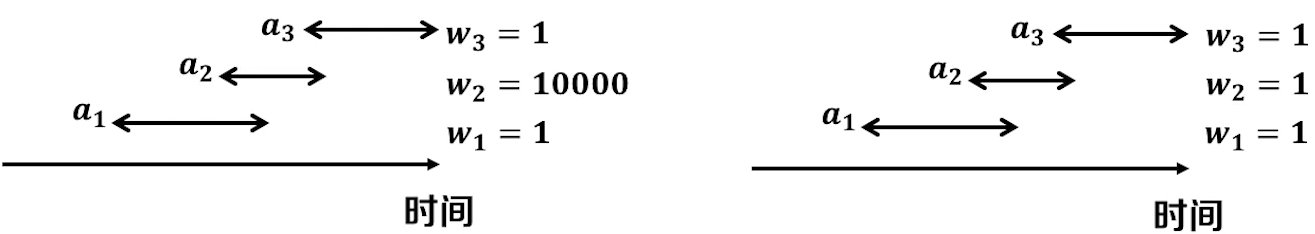活动选择问题

活动选择问题
Nuyoah活动选择问题
无权值
问题背景
有一个会场,需要安排几场活动
- 公司年会:10:00 - 19:00
- 婚礼宴请:11:00- 14:00
- 生日聚会:12:00 - 17:00
- 学术研究:14:00 - 16:00
问 如果安排这个会场能让活动尽可能的多的进行?
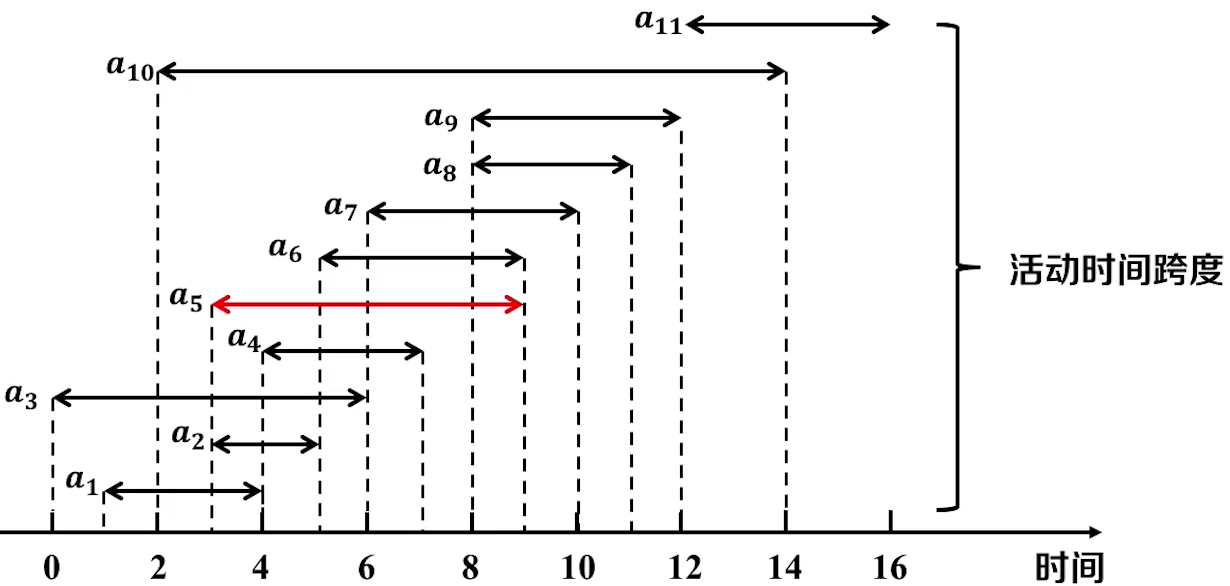
有下面这几个活动和占比时间
选择出租的时间不能有冲突
问题研究,策略选择
这时候我们采用贪心策略:
-
策略一:最短活动优先
-
策略二:最早开始的活动优先
- 策略三:最早结束活动优先
选择最早结束的活动,可以给后面的活动留出更大的弓箭
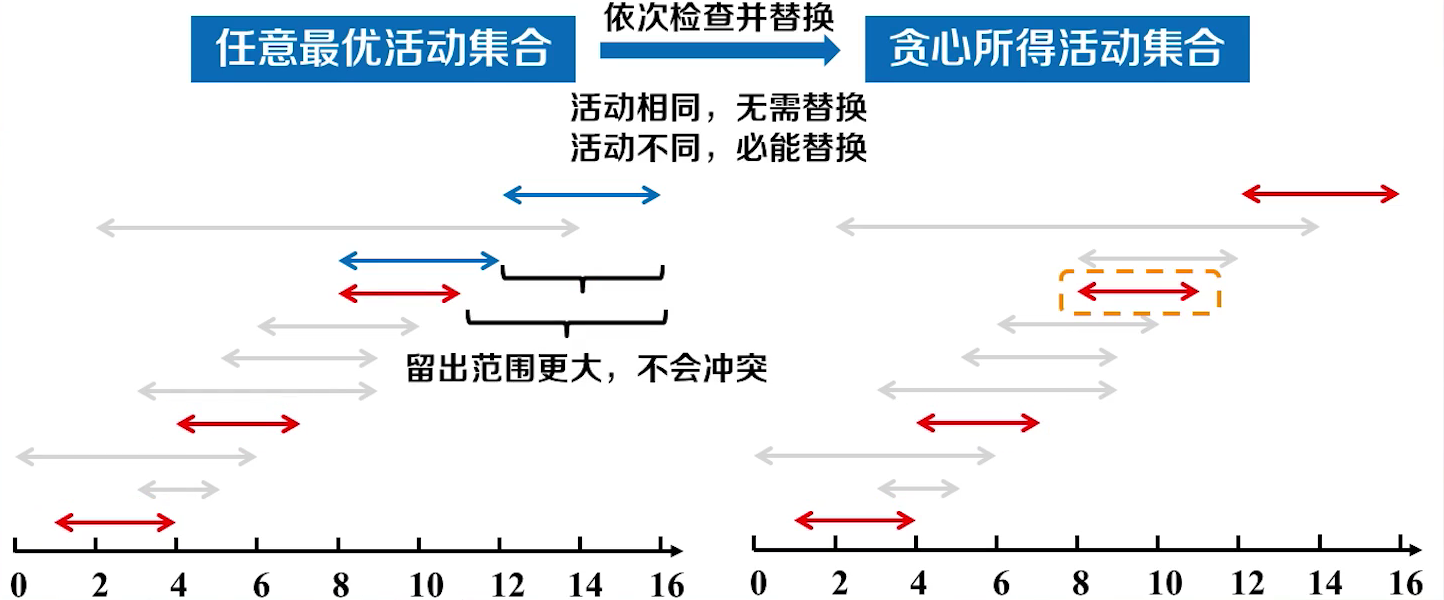
- 证明该策略是正确的(替换法)
我们可以通过替换的规则让 某个最优解替换为 贪心所得的最优解,在替换的时候,如果活动相同的话,直接替换即可,如果不相同的话,因为贪心所得的是这个活动的最先完成 的活动,所有会给后面的活动留出的活动空间更大不会影响后面活动的替换
代码实现
输入:活动集合S={a1, a2, a3 … an},每个活动ai的起始时间si 结束时间 fi
输出:不冲突的最大子集S‘
先把活动结束时间由小到大排个序
先给数组S赋值 a1(因为这里a1是最早活动的结束时间)
令K = 1
for i 循环 从2 到最后
如果 ai 的起始时间 小于 ak的结束时间的话,就把ai添加到S’中, 把 i赋值给k
最后返回 S
1 | import random |
有权值
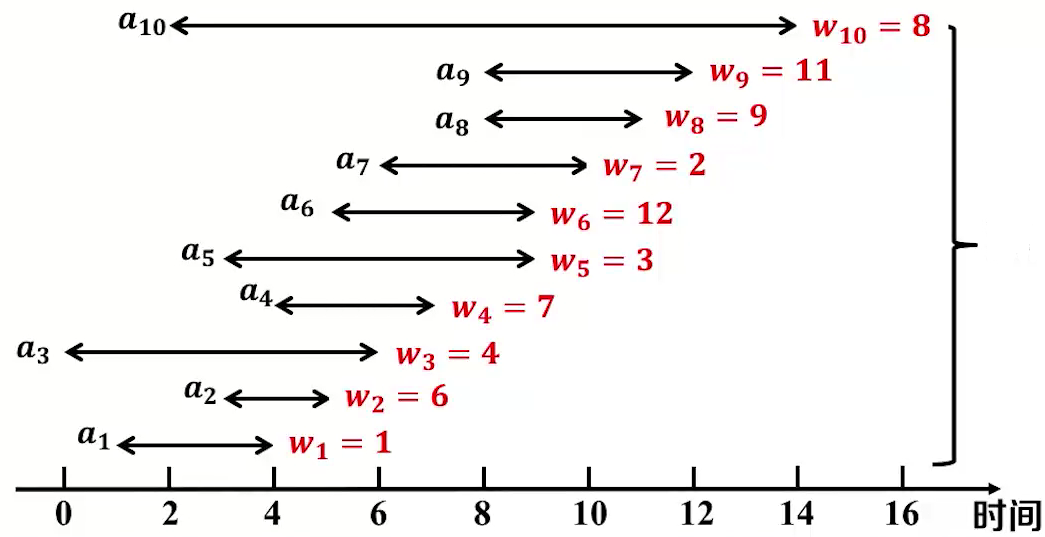
上述问题我们默认为每个事件的收入都是 1, 所以我们关注一共有多少个时间的发生:
所以相比于上面的问题我们多了一个权重:
这时候如果我们在向上面的方式来进行选择问题的话,这时候可能就会得不偿失
如果按照上述方法进行第一个问题的话 我们选择的权值和为2 , 但是实际上我们想要的权值和为 10000
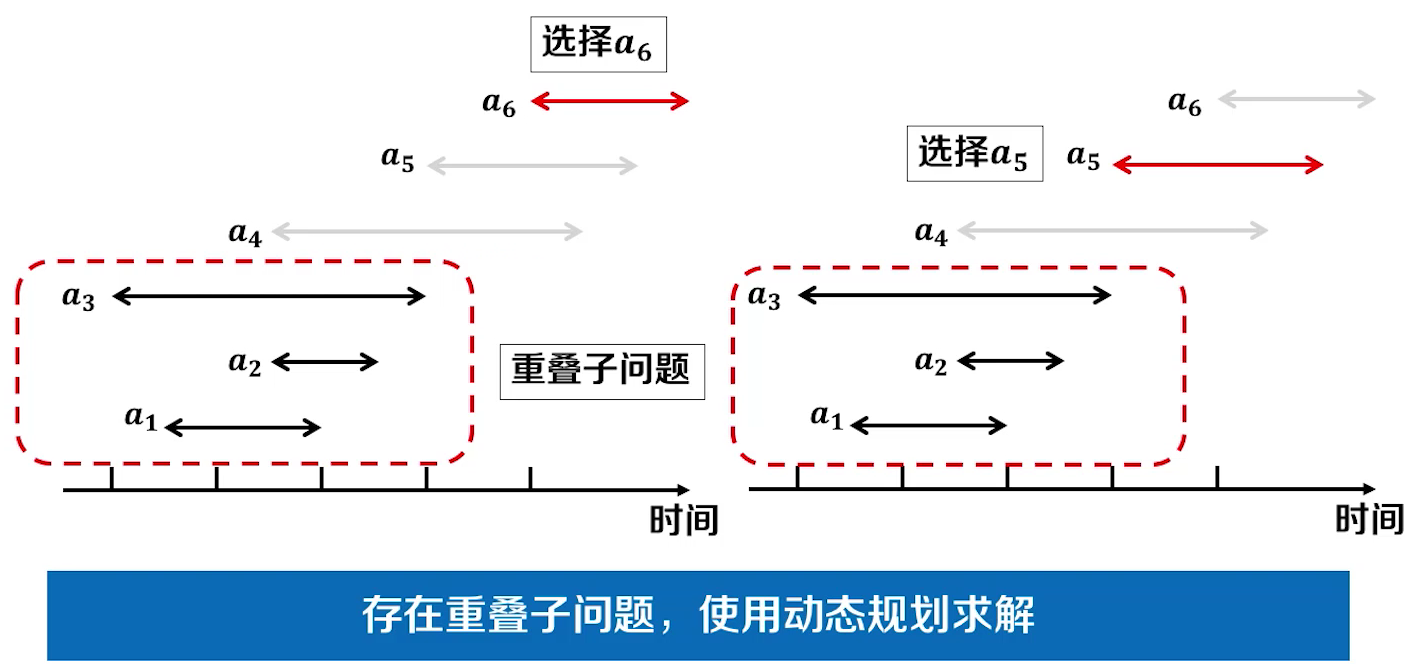
问题分析
这时候我们需要进行动态规划 + 贪心算法来求解这个问题, 选择a6 和 a5的时候我们可以根据前面的最优问题来进行求解
问题预处理
这里我们需要定义一个
p数组 p[i] 表示在a[i]开始前最后结束的活动,
p数组目的:为了防止活动冲突
D[i]数组:集合{a1, a2, a3… an}中不冲突活动的最大权值和
递推关系建立
当我们在ai的时候,
- 选择ai 那么 D[i] = Wai + D[p[i]]
- 不选择ai D[i] = D[i-1]
- 递推公式:D[i] = max{D[pi] + w, D[i-1]}
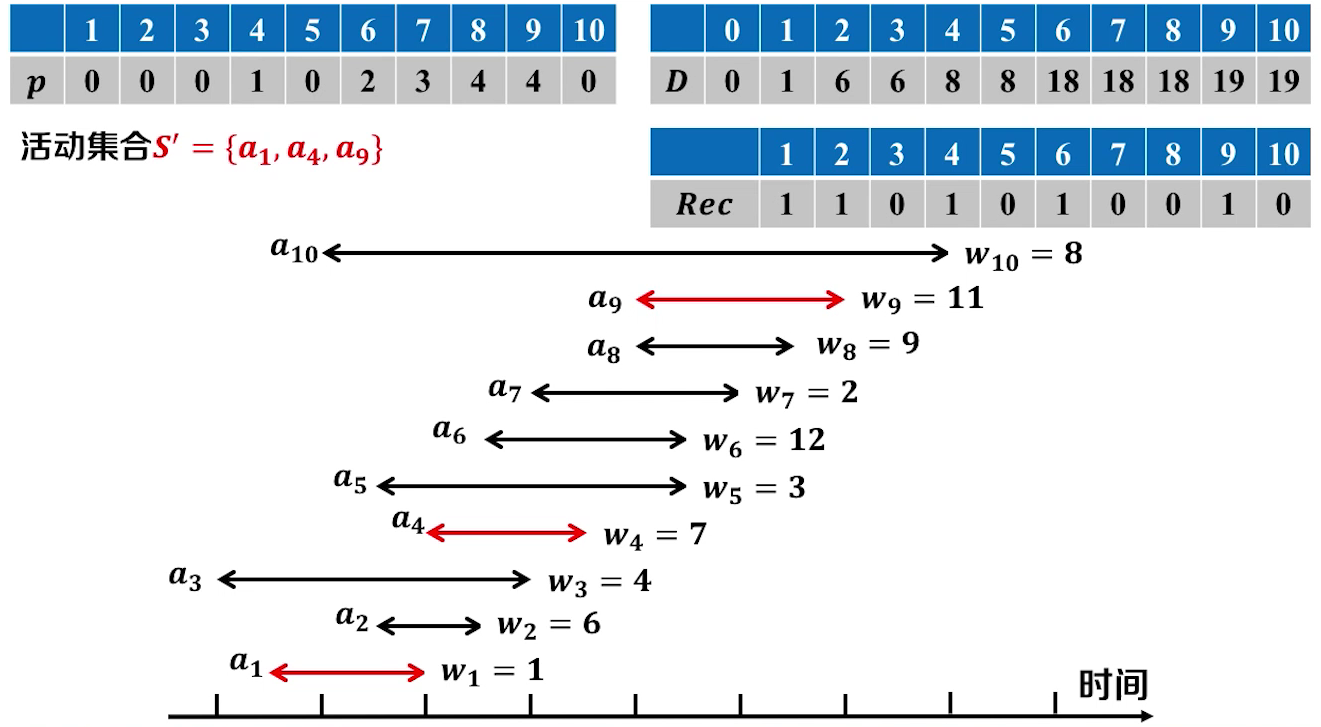
计算过程
P数组表示 ai 发生之前的最晚发生的事件
D数组表示权值的最大
Rec 1表示选择这个活动, 0表示不选择这个活动
代码实现
1 | import random |