钢条切割问题

钢条切割问题
Nuyoah钢条切割问题
问题背景
现在有一个长度为10的钢条,可以零成本 将其切割成多段长度更小的钢条,我们先要求出最大收益
| 钢条长度 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 价格p | 0 | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 24 |
如果我们不切割的话可以获得的最大收益为 24
如果我们按照 2 2 6 切割方法,收益为 27
所以不同的切割方法收益不同,我们寻求的就是收益最大的切割方法
问题定义
输入:
- 钢条的长度n
- 价格表pl(1≤ l ≤n):表示长度为l的钢条价格
输出:
- 求得一组切割方法,令收益最大化
问题观察
-
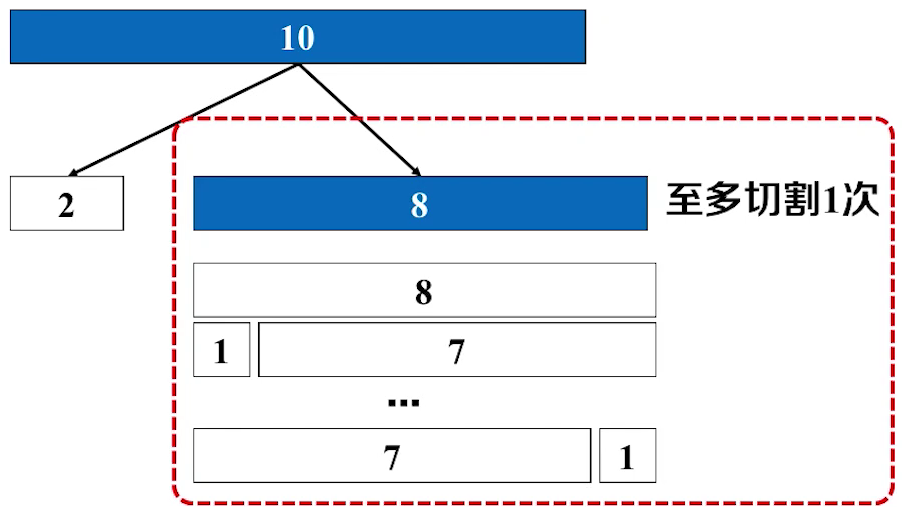
假设钢条能够至多切割一次:有以下这几种情况
我们就需要从这几种切割情况中寻找出收益最大的,max{p[i] + p[10-i], p[10]}
-
如果钢条能够切割两次:
我们可以现将钢条切割出一段
然后再剩余的钢条中继续切割
这时候 长度为8的就可以看做切割次数为一 的那一种情况
这里可能存在最优子结构 和重叠子问题
问题结构分析
问题表示:
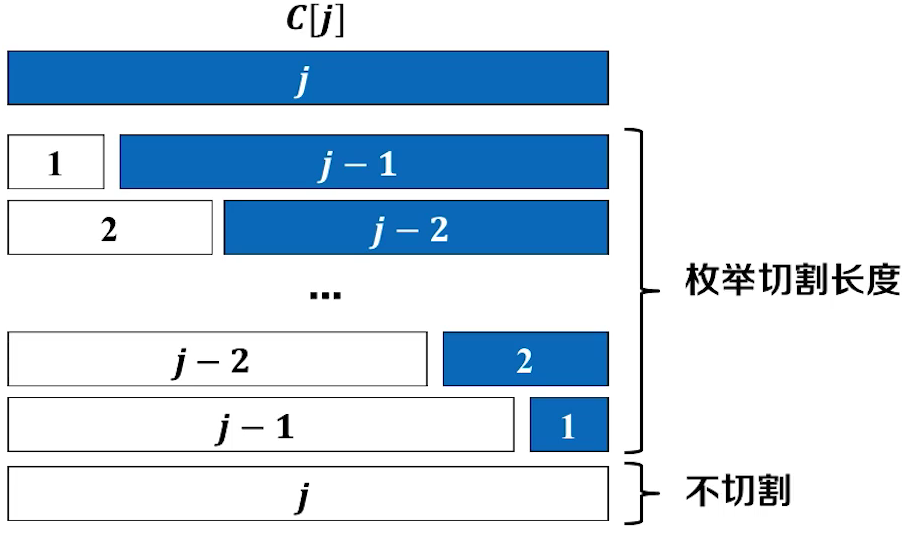
C[j]:切割长度为j的钢条可得到的最大总收益
递推关系的建立
C[j] 表示从这j种情况中选出最大的哪一种
这里面就存在最优子结构问题
自底向上的计算
我们通过 C[0] 这种情况来推断整个C数组
以后C[j] 的求导需要 依托于 C[1] ~ C[j - i] 这么多种情况中的最优解来进行C[j]的求解
所以这是一种区间性动态规划,每走一步都要依赖于一个区间的最优值
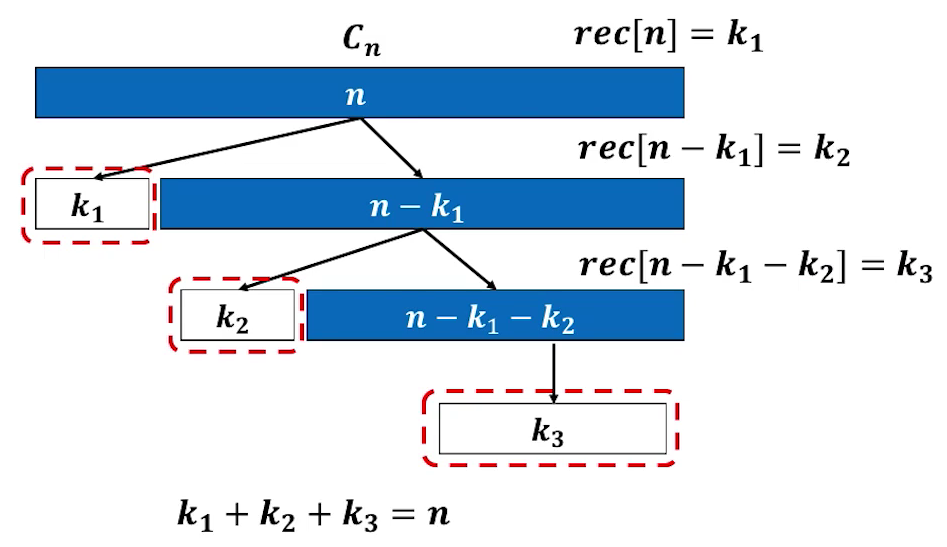
最优方案追踪
递归出口:输出的钢条长度为n
算法实例
| 钢条长度 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 价格p | 0 | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 24 |
- 我们先初始化C[0] = 0
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C[i] | 0 | ||||||||||
| rec | 0 | ||||||||||
-
钢条长度为1
这时候没得选只能够选择1
| i | 1 |
|---|---|
| 1 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C[i] | 0 | 1 | |||||||||
| rec | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 |
- 钢条长度为2:
有两种情况
- 切割一刀:结果为p[1] + C[2-1] = 2
- 不切割:结果为p[2] = 5
从上面选择情况最大的:不切割
| i | 1 | 2 |
|---|---|---|
| 2 | 5 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C[i] | 0 | 1 | 5 | ||||||||
| rec | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 2 |
- 钢条长度为3:
有三种情况:
- 在1那切割一刀:C[3] = p[1] + C[3-1] = 1 + C[2] = 6
- 在2那切割一刀:C[3] = p[2] + C[3-2] = 5 + 1 = 6
- 不切割:C[3] = p[3] = 8
从上面选择情况最大的:不切割
| i | 1 | 2 | 3 |
|---|---|---|---|
| 6 | 6 | 8 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C[i] | 0 | 1 | 5 | 8 | |||||||
| rec | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 2 | 3 |
- 钢条长度为4:
有四种情况:
-
在一那切割一刀:C[4] = p[1] + C[3] = 1 + 8 = 9
-
在二那切割一刀:C[4] = p[2] + C[2] = 5 + 5 = 10
-
在三那切割一刀:C[4] = p[3] + C[1] = 8 + 1 = 9
-
不切割:C[4] = p[4] = 9
从上面选择最大的哪一种情况:在二那切割一刀
i 1 2 3 4 9 10 9 9 i 0 1 2 3 4 5 6 7 8 9 10 C[i] 0 1 5 8 10 rec 0 1 2 3 4 5 6 7 8 9 10 1 2 3 2
- 剩下哪几种情况不在一一列举
算法实现
1 | ''' |
评论
匿名评论隐私政策
✅ 你无需删除空行,直接评论以获取最佳展示效果