算法实现算法实现0-1背包问题
Nuyoah 0-1背包问题
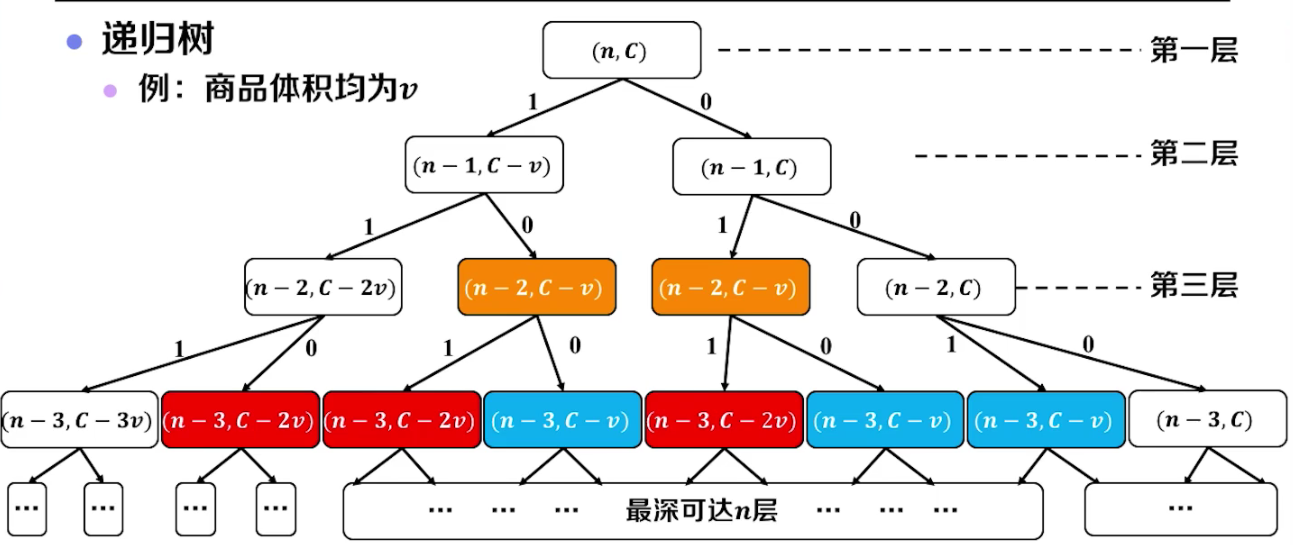
蛮力枚举法
依次列出所有可能情况!!!
n表示有n个商品, C表示容量

其中颜色相同的是需要重复计算的
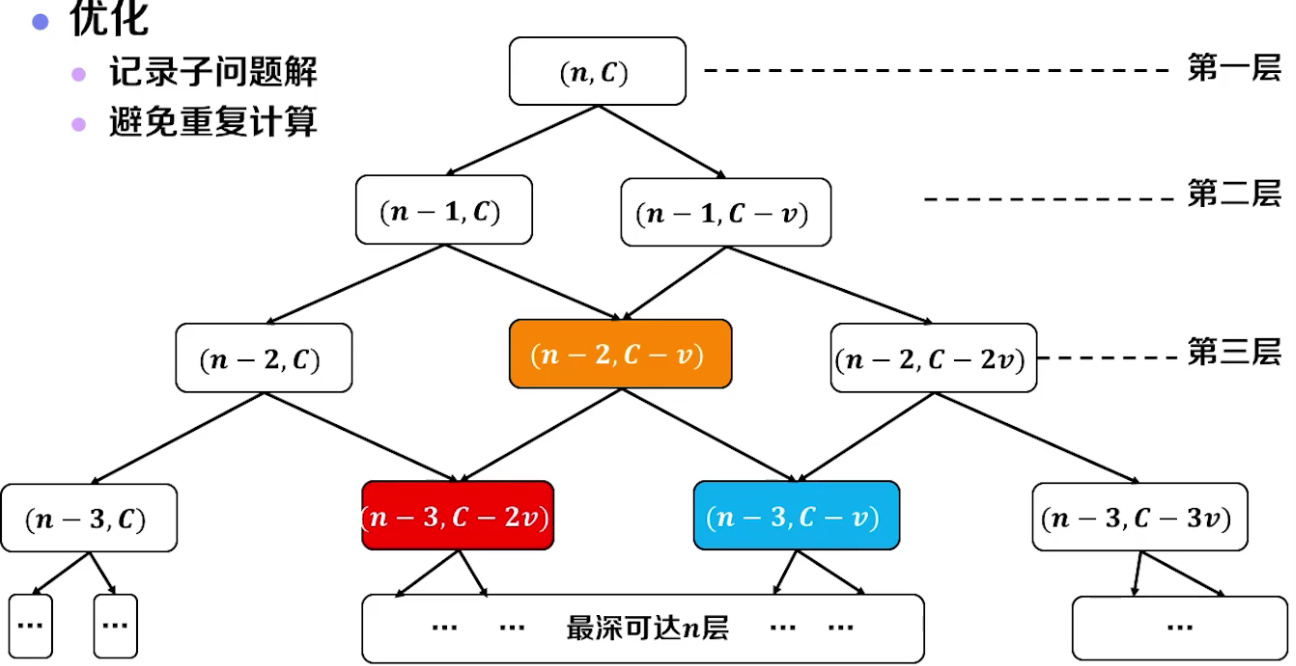
带备忘的递归
为了解决这个问题->需要大量计算重复的过程,这个时候我们可以引进一个“备忘录”,如果遇到需要重复计算的式子的话,我们可以直接重备忘录中获取。

伪代码的实现:
KnapsackMR(i, c)
1
| if(c < 0) then 容量为零 返回负无穷
|
1
| if i ≤ 0 then 如果商品的个数小于零的话,返回零
|
1
| if P[i, c] ≠ NULL then 如果备忘录中有这个的话就不用计算 直接返回即可
|
1
| P1 = KnapsackMR(i-1, c-vi)
|
1
| p[i, c] <= max{P1 + pi, P2}
|
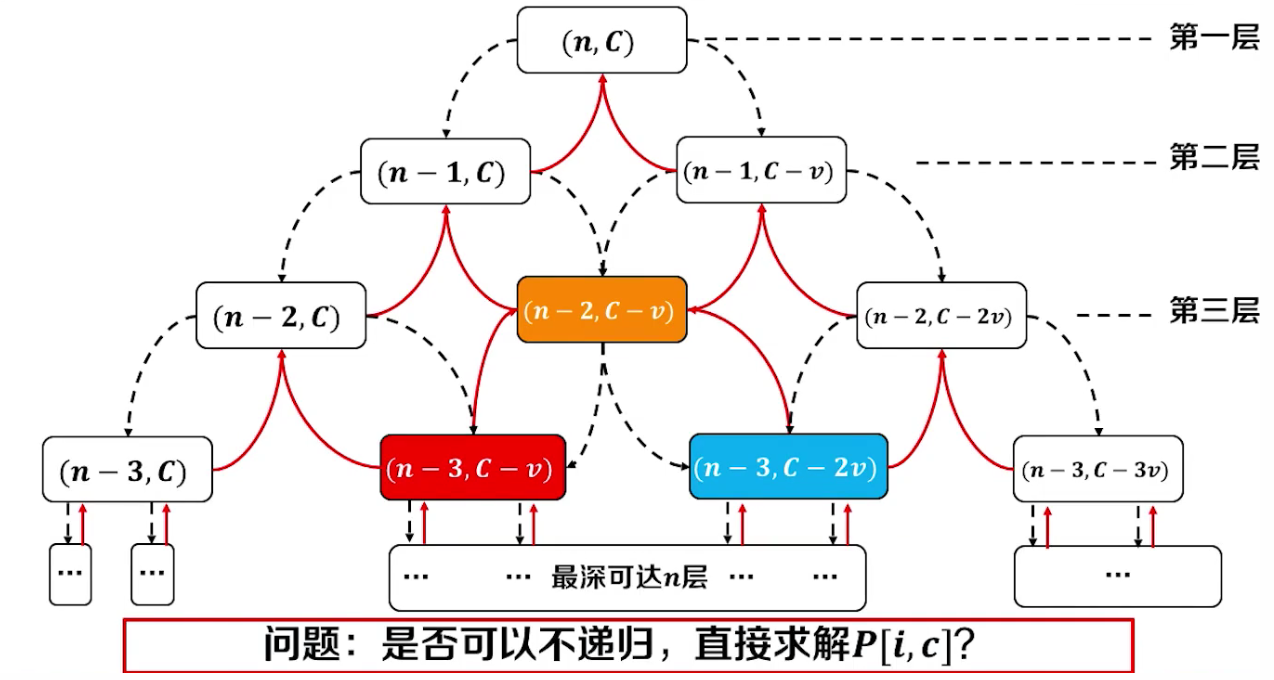
计算顺序:

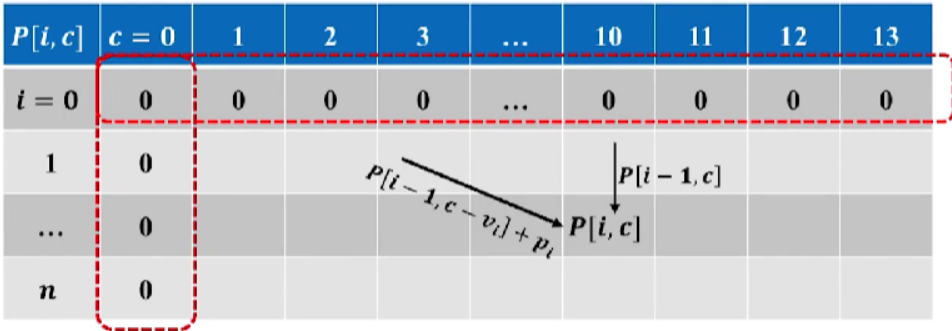
为了能够不递推,直接求解P[i,c],这就需要我们事先把备忘录表,全部填写上去
p[i,c]确定的方法需要让p[i-1, c]和p[i-1,c-vi]+pi 相比较,选取其中较大的哪一个

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
|
def memo_rec_matrix(num_commodity, size_knapsack, Price):
memo = [ [ [] for i in range(size_knapsack+1)] for m in range(num_commodity+1)]
rec = [ [ [] for i in range(size_knapsack+1)] for m in range(num_commodity+1)]
for m in range(size_knapsack+1):
memo[0][m] = 0
rec[0][m] = 0
for m in range(num_commodity+1):
memo[m][0] = 0
rec[m][0] = 0
for i in range(1, num_commodity+1):
for m in range(1, size_knapsack+1):
if m < Price[0][i-1]:
memo[i][m] = memo[i-1][m]
rec[i][m] = 0
else:
if memo[i-1][m] > memo[i-1][m-Price[0][i-1]]+Price[1][i-1]:
memo[i][m] = memo[i-1][m]
rec[i][m] = 0
else:
memo[i][m] = memo[i-1][m-Price[0][i-1]]+Price[1][i-1]
rec[i][m] = 1
return memo, rec
def track(rec, price):
rec_num_line = len(rec)-1
rec_num_column = len(rec[0])-1
while(True):
if rec_num_line == 0:
break
elif rec[rec_num_line][rec_num_column] == 0:
rec_num_line -= 1
else:
print(rec_num_line)
rec_num_line -= 1
rec_num_column -= price[0][rec_num_line]
price = [
[10,3,4,5,4],
[24,2,9,10,9]
]
num_commodity = 5
size_knapsack = 13
memo, rec = memo_rec_matrix(num_commodity,size_knapsack,price)
|